Policy Optimization - Part 0
Policy based algorithms have gained quite some popularity. With usage across continuous space-continuous actions, these algorithms cater to wide variety of problems ranging from systematic trading algorithms to self-driving cars. So, what are these policy based algorithms and why are they gaining such popularity. This series of articles is dedicated to explaining wide variety of Policy Gradient algorithms.
A quick recap on Value based agents
As we have read that Value based learnings (such as Q-learning, DQN, DDQN etc.) algos aim to maximize the state-value (or action-value).
\(V^\pi(s) = \mathbb{E} [R|s, \pi]\)
\(V^*(s) = max_\pi V^\pi(s)\).
In DQN (or any other value based learning agent), the objective is to maximize value functions.
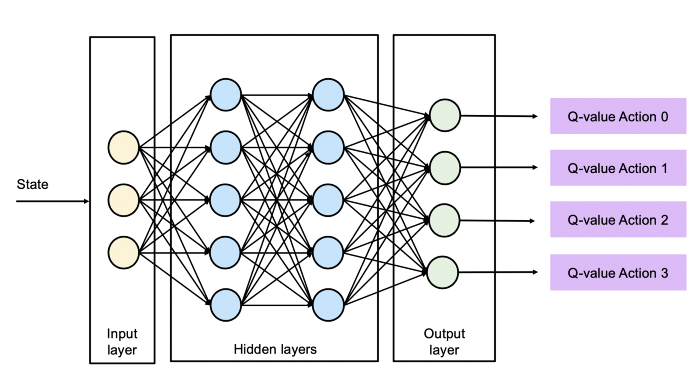
But such agents come with certain challenges of their own:
- Limited to Discrete Action space problems.
- Slower convergence
- Exploration Exploitation dilemma
- Experience Memory maintenance
Although algos such as DQN, DDQN are state of the art algorithms in their capacity, but Policy Gradient (PG) Algorithms provide an edge over them. Let’s see how!
So, what are Policy Gradient Algorithms
We have been using \(\pi({a/s}, \theta)\) as our policy. But, we never thought of directly optimizing the policy.
Objective: \({max} {J}(\theta)\) where ${J} {, } \theta$ refer to performance measure and policy parameters respectively.
We can use stochastic gradient ascent methods to solve this optimization problem. I will not go into mathematical details as there is a lot of literature available on that. In short, here is what comes out as policy gradient algorithm:
\(\nabla_\theta{J}(\theta) \propto {G}.\nabla_\theta{log}\pi_\theta(s/a)\) \(\theta_{t+1} = \theta_{t} + \alpha.G_t.\nabla_\theta{log}\pi_\theta(s/a)\)
Key takeaways from above equation:
- $ \nabla_\theta{J} $ is independent of states distribution.
- $ \theta $ is updated in proportion to return. If higher return is achieved by taking a particular action, then the probability of taking that action rises in proportion.
Why would I choose Policy Based over Value Learning Agent?
PG methods provide quite a few valid reasons why I should choose them. Mind that the list is not exhaustive. I will add more as I stumble upon more advanatges:
- Faster convergence, Well, who doesnt like it?
- Can cater to high dimensions and continuous state-action space environments. Becomes handy with real-life situations. I cant always take a 90 degree left turn (an action) while driving my car.
- Can learn Stochastic Policies. In simple words, you choose action from a distribution.
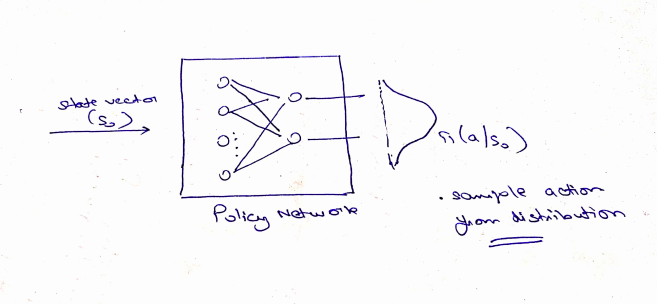
Conclusion
With aforementioned advantages, it makes sense to take a deep dive into various Policy optimization techniques. The next few articles in this series are dedicated to individual algorithms along with their usage. So, sit back and relax while you move along the exciting world of Reinforcement Learning!
Appendix
1. Notations
Mathematics isn’t fun without complex equations :)
So, here is the summary of all variables used in various equations related to Policy Optimization.