Fractals - A brief primer
Few years back, I had written my first article on Fractals. At that time, I had never thought that I would be mesmerized by the beauty of it!
Fractals have helped to find and understand a pattern in this chaotic universe. Nature doesn’t follow a fractal behaviour; however a fractal model best explains the structure of such a complex pattern. Fractal theory has found its application in every aspect of technology, be it Computer graphics, Communications, Modeling landscapes, as well as Finance.
This article will present an understanding on Fractals in most basic terms, and how we can design our own fractals.
What are Fractals
Students are taught only about the Euclidean space, where objects can be observed in 0, 1, 2, 3 (or higher integral) Dimensions.
- 0-Dimension –> a point
- 1-Dimension –> a line (anything plotted on just a single axis)
- 2-Dimension –> a square, a circle (or anything plotted on x-y plane)
- 3-Dimension –> a cube, a sphere (or anything plotted on xyz surface)
But, ever heard of a fractional dimension? How about a 1.26-D figure? How will it look? Or, can we even describe a dimension in fractional terms?
That brings us to Fractals. Derived from the word fractional, it literally means an object have a fractional dimension. A well know example of British Coastline, also known as ‘Coastline paradox’, is a general idea of Fractals. The coastline of Britain can’t be calculated accurately with a particular scale length. As the scale size decreases, it uncovers more intricate parts of the coastline, and the length changes. This leads to the idea of Scaling, a well know Scaling law and the concept of Fractal Dimensions.
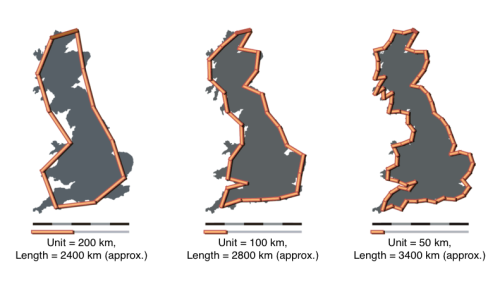
Scaling law highlights the fact that as we reduce the size of measuring stick, the number of sticks required to measure the length is given by: \(N = k * (1/s)^D\)
Let’s look at couple of examples of basic Fractals and associated Fractal dimensions.
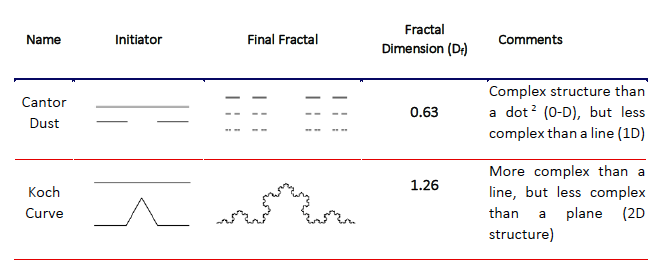
In its simplicity, these designs have dimensions 0.63 and 1.26 respectively. How can we design these fractals on our own?
Decoding the design of Fractals
Fractals are self-similar and self-affine designs. Mathematically, it involves deep understanding of Linear Algebra, and few concepts of Set theory. But, the aim here is not to dwell into complex form of mathematics, but to simplify and visualize the maths instead.
A simple case of Koch Flake, helps explain what a fractal would look like when you zoom it infinitely. You will see the same pattern over and over again, confirming the case of self similarity.

Visualize it step by step
So, lets visualize the mathematics of Fractals here.
Considering the self similar attribute, it can be observed that a Koch flake includes various design components
- To begin with, we have a triangle.
- For each side of the triangle, below transformations are done:
- Transformation 1: Size reduced to one-third.
- Transformation 2: Size reduced to one-third and a clockwise rotation of 60 degrees
- Transformation 3: Size reduced to one-third and a counter clockwise rotation of 60 degrees.
- Transformation 4: Size reduced to one-third.
- Repeat Step 2 iteratively.
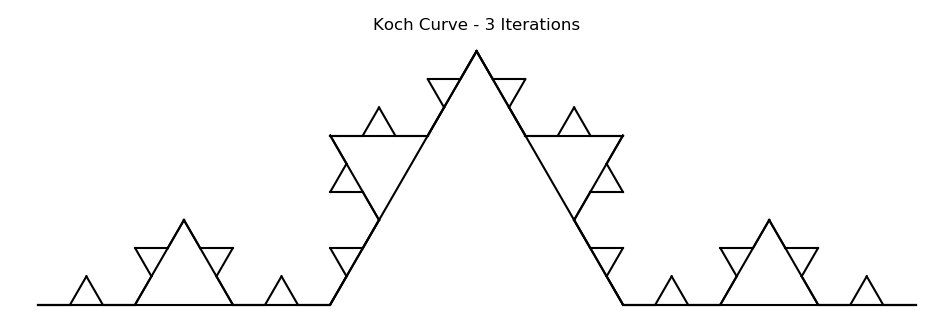
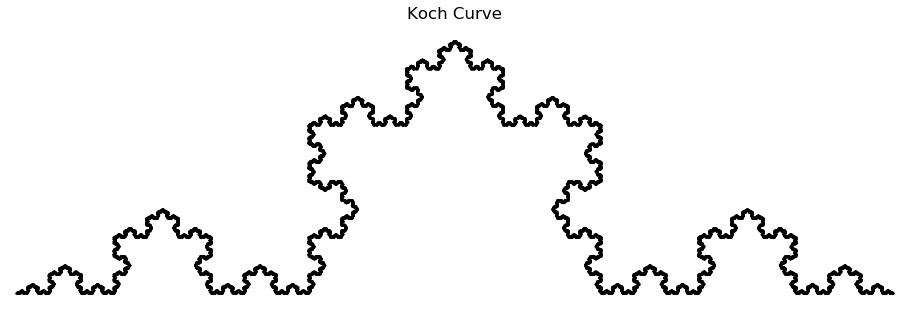
What to conclude from here?
Fractals have found its way into modeling of natural objects, explaining things which can’t be explained by existing knowledge of mathematics. Fractal Theory, since 1970s, has been developed and continuous research is being done in this area. These fractals are considered as objects that exist between dimensions.
Fractologists (yeah, I am coining this word now) have gone quite far in the research in all aspects known. With applications in Computer vision, Modeling chaotic Landscapes, Networks Engineering, Time series modeling and more importantly Finance, fractals theory in now finding its way to define randomness.
Subsequent articles will elaborate more of the designing of these complex patterns, before moving onto their usage in Finance.