Numerical Methods - Comparing different FDMs
In the first 3 articles, we explored Explicit and Implicit and Crank Nicholson schemes.
This article primarily focuses on comparing them more closely and understand theri respective Finanical use cases if any.
Comparison Summary
| Feature | Explicit Euler | Implicit Euler | Crank-Nicolson |
|---|---|---|---|
| Stability | Conditionally stable (small \(\Delta t\)) | Unconditionally stable | Unconditionally stable |
| Accuracy (Time) | First-order accurate | First-order accurate | Second-order accurate |
| Accuracy (Space) | Second-order accurate | Second-order accurate | Second-order accurate |
| Computational Cost | Low (no system solving) | High (solves system of equations) | High (solves system of equations) |
| Implementation | Simple to implement | More complex (requires solver for systems) | More complex (requires solver for systems) |
| Suitability | Best for problems where time steps are small | Best for stability with large time steps | Best for balanced stability and accuracy |
| Use Cases | Simple problems, fast but less accurate | Stiff problems, large time steps | More accurate problems, balanced solution |
Let’s look at each of these differences one by one, and try to understand what they mean.
a. Stability
We already covered Stability and respective issues in individual articles, and it is evident that
- Implicit and Crank Nicholson provides unconditional stability irrespective of how small the time steps be.
- Explicit, on the other hand, behaves erratically when \(\Delta t\) goes small, as was seen with the option price blowing up, and gamma values jumping at the boundary values of underlying
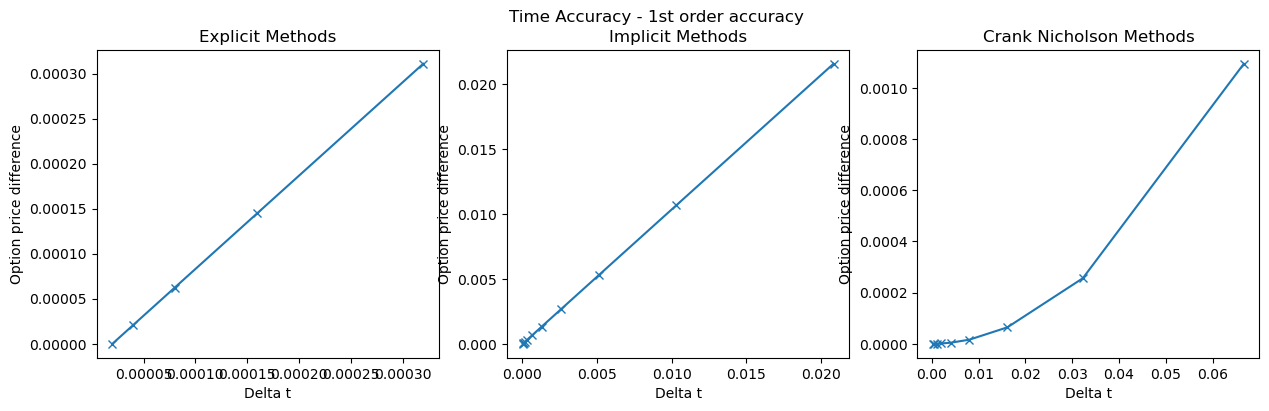
b. Time Accuracy
As the time grid compacts, i.e. \(\Delta t\) reduces, how does the numerical approximation improves? That’s the crux of time accuracy.
In numerical methods, the time accuracy refers to how well the time derivatives i.e., the terms involving the time variable are approximated by the finite difference scheme. The time order accuracy quantifies how the error in the time discretization decreases as the time step \(\Delta t\) becomes smaller.
The case of Explicit and Implicit provide a 1st order accuracy in time. On the other hand, Crank Nicholson showcases a 2nd order time accuracy. What it means is if by just halving the \(\Delta t\), we get \(\frac {1}{4}\) improvement in option price with Crank Nicolson.
Info
In order to estimate the order of time accuracy, the exact solution of Option price is approximated using Taylor expansion. At the same time, we approximate the option price using numerical method. Difference in the price of these 2 processes help estimate the time accuracy
Mathematical explanation for Implicit Method. Caution: A bit technical
Let \(V_{n+1} \) denote the option value at time \( {n+1} \) in discretized manner, and \( V(t_{n+1}) \) in the actual continuos fashion.Step 1: Continuous manner value can be approximated as using Taylor Series: \[ V(t_{n+1}) = V(t_n) + \Delta t \frac{\partial V}{\partial t} \bigg|_{t_n} + \frac{\Delta t^2}{2} \frac{\partial^2 V}{\partial t^2} \bigg|_{t_n} + O(\Delta t^3) \] Step 2: The discretized form of the time derivative for the Implicit Euler method is: \[ \frac{V_{n+1} - V_n}{\Delta t} = L(V_{n+1}) \] Rearranging to solve for \( V_{n+1} \): \[ V_{n+1} = V_n + \Delta t L(V_{n+1}) \] Here, \( L(V_{n+1}) \) represents the discretized spatial derivatives at time step \( t_{n+1} \).
Step 3: Now we expand \( L(V_{n+1}) \) (the spatial operator) in a Taylor series around \( t_n \): \[ L(V_{n+1}) = L(V(t_n)) + \Delta t \frac{\partial L(V)}{\partial t} \bigg|_{t_n} + O(\Delta t^2) \] Substituting this into the Implicit Euler scheme: \[ V_{n+1} = V_n + \Delta t \left[ L(V(t_n)) + \Delta t \frac{\partial L(V)}{\partial t} + O(\Delta t^2) \right] \] Simplifying the expression: \[ V_{n+1} = V_n + \Delta t L(V(t_n)) + O(\Delta t^2) \] Step 4: Comparing with Exact Solution
The exact solution at time \( t_{n+1} \) is: \[ V(t_{n+1}) = V(t_n) + \Delta t \frac{\partial V}{\partial t} + \frac{\Delta t^2}{2} \frac{\partial^2 V}{\partial t^2} + O(\Delta t^3) \] Now, compare this with the Implicit Euler update: \[ V_{n+1} = V_n + \Delta t L(V(S,t_n)) + O(\Delta t^2) \] The difference between the exact solution and the Implicit Euler solution is the error: \[ \text{Error} = V(t_{n+1}) - V_{n+1} \]
c. Space Accuracy
In numerical methods, the space accuracy refers to how well the space derivatives i.e., the terms involving the space variable are approximated by the finite difference scheme. The space order accuracy quantifies how the error in the time discretization decreases as the space step \(\Delta S\) becomes smaller.
As the space grid compacts, i.e. \(\Delta S\) reduces, how does the numerical approximation improves? That’s the crux of space accuracy. All three methods exhibit similar performance here.
d. Computation Cost and Implementation
We already checked the mathematical formulation for each method in the respective topics. Its quite evident that Explicit is simplest of all, both in terms of mathematics as well as implementation. However, both Implicit and Crank Nicholson both need matrix computations to solve system of equations iteratively. It makes the whole process computationally extensive
What’s next?
Finite Difference methods have been there for over 6 decades, and still are extremely useful in multiple use-cases. We uncovered some of the techniques in FDM such as Explicit, Implicit and Crank Nicholson schemes. Besides these famous ones, there are many other Numerical methods to solve Partial differential equations, naming a few of them as below.
I. Finite Difference Methods
- i. Explicit
- ii. Implicit
- iii. Crank Nicholson
- iv. Modified Theta (A generalized version of all above 3)
- v. Exponential Fitted Schemes, (such as Duffy)
- vi. Douglas Scheme
- vii. Leapfrog (primarily for 2nd order time derivative PDE)
II. Finite Element Method
III. Finite Volume Method, etc.
Besides, there are now Neural networks based PDE solvers that can provide a robust solution, however, unlike Numerical methods, they dont offer any transparency.
Summary
For simple problems such as Vaniall call option, we will not make use of any approximate solutions as a closed form exist for them. However, when a process becomes more complex in nature, such as a path dependent Barrier option or a process which involves jumps as well, such as Jump diffusion models, Crank Nicholson can come handy to provide more accurate solution.
Math Concepts
Listing down some of the mathematical concepts referred in this article
- Time and Space Accuracy
Appendix
- Research Details & Source: Project Quant, by Ankit Gupta
- Finite Difference Methods in financial engineering, A Partial Differentiation Equation Approach, by Daniel J Duffy
PS: For detailed python notebook, you can reach out to me directly!
Disclaimer: The article is solely made available for educational purposes and doesn't promote any investment or trading guidance whatsoever. Any views or opinions presented in this article are solely those of the author.
