Numerical Methods - Crank Nicholson Method
In the last 2 articles, we explored Explicit and Implicit methods. What if we have the best of 2 worlds.
Crank Nicholson scheme is nothing but a combination of both the methods, with equal proportion. This article goes in a bit of depth of this scheme.
Again, starting with the summary of Black Scholes Equation for Call option pricing
Summary of Black Scholes PDE Note In later articles, we will try to value a more complex derivative product, such as Barrier option or a Equity-Credit Hybrid product with a more complex initial value.Backward Black Scholes PDE
$$ % \begin{aligned} -\frac{\partial V}{\partial t'} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 % \end{aligned} $$ Initial Value problem
For a European call option: $$ % \begin{aligned} V(S, 0) = \max(S_T - K, 0) % \end{aligned} $$Boundary Conditions
In the case of boundary conditions, we tend to find option values at extreme ends of stock price. $$ % \begin{aligned} V(0, t) = 0 \\ V(S_{max}, t) = S_{max} - K e^{(-rt)} % \end{aligned} $$
Crank Nicholson - The Theory
Just like the Explicit Euler Scheme, here also, we will follow a trinomial lattice model. However, unlike the Explicit Scheme, where the process at time (t) was dependent on the previous time step (t-1), in Implicit Scheme, the process is dependent on the current time step. It can be better explained in a visual form.
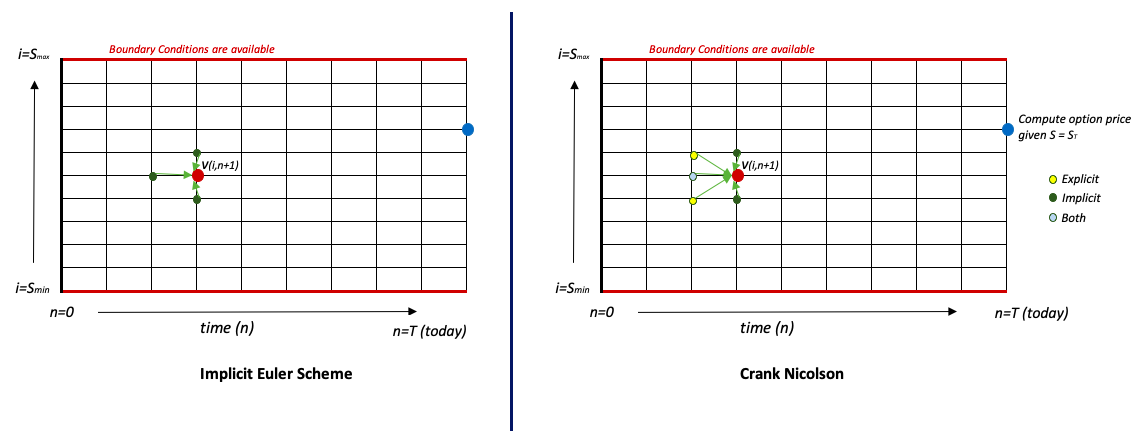
The left panel describes the Implicit Scheme, whereas the right panel highlights Crank Nicholson Euler Scheme. Clearly indicates that Crank Nicholson utilizes both Explicit and Implicit schemes.
Note
V(i,n+1) depends on 5 points. In order to determine the price at current time and stock price, we need the prices at current time with shocks in the stock price (up and down). That's the crux of Implicit Euler Scheme. And this makes the solution a bit more complex than pure iterations.
- V(i-1, n+1): option value at \( S = S_{i-1} \) and current time
- V(i+1, n+1): option value at \( S = S_{i+1} \) and current time
- V(i, n): option value at \( S = S_{i} \) and previous time
- V(i-1, n): option value at \( S = S_{i-1} \) and previous time
- V(i+1, n): option value at \( S = S_{i+1} \) and previous time
Discretized Black Scholes - Application in Finance
a. Time derivative
Here, \(n+1\) refers to forward in time, using forward difference method —> \(\frac{\partial v}{\partial t'} \approx \frac{v_i^{n+1} - v_i^n}{\Delta t'}\)
b. Spatial derivative (2nd order)
For the second spatial derivative \(\frac{\partial^2 v}{\partial S^2}\), we use the combination of Explicit and Implicit Schemes \[% \begin{aligned} \frac{\partial^2 v}{\partial S^2} \approx \frac{Explicit + Implicit}{2} \\ % \end{aligned}\]
where \[% \begin{aligned} Explicit \approx \frac{v_{i+1}^{n} - 2v_i^{n} + v_{i-1}^{n}}{(\Delta S)^2} \\ Implicit \approx \frac{v_{i+1}^{n+1} - 2v_i^{n+1} + v_{i-1}^{n+1}}{(\Delta S)^2} % \end{aligned}\]
Note
Here, we give equal weightage to both the schemes. A more generalized version is Modified Theta Method, where \( \theta \) presents the ratio between the both the schemes.
\( \frac{\partial^2 v}{\partial S^2} \approx \theta \cdot (\text{Explicit}) + (1 - \theta) \cdot (\text{Implicit}) \)
c. Spatial derivative (1st order)
For the first spatial derivative \(\frac{\partial v}{\partial S}\), we use the below \[% \begin{aligned} \frac{\partial v}{\partial S} \approx \frac{Explicit + Implicit}{2} \\ % \end{aligned}\]
where \[% \begin{aligned} Explicit \approx \frac{v_{i+1}^{n} - v_{i-1}^{n}}{2 \Delta S} \\ Implicit \approx \frac{v_{i+1}^{n+1} - v_{i-1}^{n+1}}{2 \Delta S} % \end{aligned}\]
d. Spatial process (without derivative)
\[% \begin{aligned} v_{i} = \frac{1}{2} (v_{i}^{n} + v_{i}^{n+1} ) % \end{aligned}\]e. Black Scholes discretization
Expand for more...
Hence, under the Crank Nicholson Scheme, the Backward Black Scholes can be approximated as: $$ % \begin{aligned} -\frac{v_i^{n+1} - v_i^n}{\Delta t} + \frac{1}{2} \left\{ \frac{1}{2} \sigma^2 S_i^2 \frac{v_{i+1}^{n+1} - 2v_i^{n+1} + v_{i-1}^{n+1}}{(\Delta S)^2} + \frac{1}{2} \sigma^2 S_i^2 \frac{v_{i+1}^{n} - 2v_i^{n} + v_{i-1}^{n}}{(\Delta S)^2} \right\} + \frac{r S_i}{2} \left\{ \frac{v_{i+1}^{n+1} - v_{i-1}^{n+1}}{2 \Delta S} + \frac{v_{i+1}^{n} - v_{i-1}^{n}}{2 \Delta S} \right\} - \frac{r}{2} \left\{ v_i^{n+1} + v_i^{n}\right\} = 0 % \end{aligned} $$ Rearrange this equation to isolate the terms involving \( v^{n+1} \) on left side, and \( v^{n} \) on right side. $$ % \begin{aligned} v_{i-1}^{n+1} (\alpha_i \Delta t) + v_i^{n+1}(1 - \beta_i \Delta t) + v_{i+1}^{n+1} (\gamma_i \Delta t) = v_{i-1}^{n}(-\alpha_i \Delta t) + v_i^{n}(1 + \beta_i \Delta t) + v_{i+1}^{n} (-\gamma_i \Delta t) % \end{aligned} $$ Wheree. Matrix Formulation
Step 1 - Linear System of Equations
It is easier to visualize the system as a set of equations at \( t = n+1 \), where \( i \) varies from 1 to \( I-1 \). The system can be written as: \[ \begin{aligned} v_{0}^{n+1} (\alpha_1 \Delta t) + v_1^{n+1}(1 - \beta_1 \Delta t) + v_{2}^{n+1} (\gamma_1 \Delta t) &= v_{0}^{n} (-\alpha_1 \Delta t) + v_1^{n}(1 + \beta_1 \Delta t) + v_{2}^{n} (-\gamma_1 \Delta t) \\ v_{1}^{n+1} (\alpha_2 \Delta t) + v_2^{n+1}(1 - \beta_2 \Delta t) + v_{3}^{n+1} (\gamma_2 \Delta t) &= v_{1}^{n} (-\alpha_2 \Delta t) + v_2^{n}(1 + \beta_2 \Delta t) + v_{3}^{n} (-\gamma_2 \Delta t) \\ &\vdots \\ v_{I-2}^{n+1} (\alpha_{I-1} \Delta t) + v_{I-1}^{n+1}(1 - \beta_{I-1} \Delta t) + v_{I}^{n+1} (\gamma_{I-1} \Delta t) &= v_{I-2}^{n} (-\alpha_{I-1} \Delta t) + v_{I-1}^{n}(1 + \beta_{I-1} \Delta t) + v_{I}^{n} (-\gamma_{I-1} \Delta t) \end{aligned} \]Step 2-4 - Matrix Formulation and Solving the matrix
This can be conveniently represented in matrix form as:\( A \cdot X = B \). This can be done similar to how we did it in the case of Implicit Methods
Codify Crank Nicholson - Black Scholes
Here is a sample python code depicting Implicit Euler Scheme:
# relevant libraries for matrix algebra
from scipy import sparse
from scipy.sparse.linalg import spsolve
from importlib import reload
import numpy as np
# Setting the initial parameters
def CrankNicholson(SMax, SMin, nbSpaceSteps, timetoMaturity, nbTimeSteps, vol, rate, strike, optiontype = "call"):
# initializing the space and time vectors for the grid
S = np.linspace(SMin, SMax, nbSpaceSteps + 1)
dS = (SMax - SMin)/nbSpaceSteps
time = np.linspace(0, timetoMaturity, nbTimeSteps + 1)
dt = (timetoMaturity - 0)/nbTimeSteps
# nbTimeSteps = int(timetoMaturity/dt)
# setting the storage grid for derivative price
V = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
delta = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
gamma = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
theta = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
# ------ Setting initial condtion
# initial condition
if optiontype.upper()[0] == "C":
V[:,0] = np.maximum(S - strike, 0)
else:
# for put option
V[:,0] = np.maximum(strike - K, 0)
# boundary condition
if optiontype.upper()[0] == "C":
V[0, :] = 0
V[-1, :] = SMax - (strike)*np.exp(-rate*time)
else:
V[-1, :] = 0
V[0, :] = (strike)*np.exp(-rate*time) - SMin
# apply Crank Nicholson Scheme
I = np.arange(0,nbSpaceSteps+1)
alpha = 0.25 * dt * ((vol**2) * (I**2) - rate*I)
beta = -dt * 0.5* (vol**2 * (I**2) + rate)
gamma = 0.25 * dt * (vol**2 * (I**2) + rate * I)
# creation of sparse matrices
ML = sparse.diags([-alpha[2:], 1-beta[1:], -gamma[1:]], [-1,0,1], shape=(nbSpaceSteps-1, nbSpaceSteps-1)).tocsc()
MR = sparse.diags([alpha[2:], 1+beta[1:], gamma[1:]], [-1,0,1], shape=(nbSpaceSteps-1, nbSpaceSteps-1)).tocsc()
for t in range(1, nbTimeSteps+1):
# Applying the boundary conditions
boundary_t = np.zeros(nbSpaceSteps - 1)
boundary_t[0] = alpha[1] * (V[0, t-1] + V[0, t]) #-alpha[0] * V[0, t - 1]
boundary_t[-1] = gamma[nbSpaceSteps - 1] * (V[nbSpaceSteps, t] + V[nbSpaceSteps, t-1] )
B = MR.dot(V[1:nbSpaceSteps, t - 1])
b = B + boundary_t
# Solve for the matrix
V[1:nbSpaceSteps, t] = spsolve(ML, b)
return S, time, V
# -------- Compute the call price using Crank Nicholson scheme
SMax = 200
SMin = 0
timetoMaturity = 1
vol = 0.2
rate = 0.05
nbSpaceSteps = 400
nbTimeSteps = 100
strike = 100
S0 = 100
S, _time, callPrice = CrankNicholson(SMax, SMin, nbSpaceSteps, timetoMaturity, nbTimeSteps, vol, rate, strike, optiontype = "call")
Results
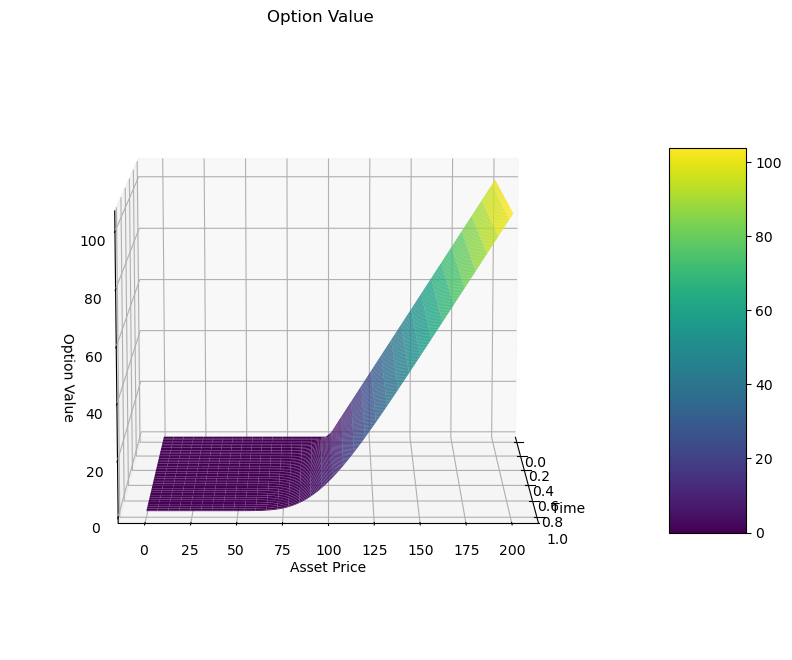
a. Option Valuation
Plot looks similar to Implicit and Explicit schemes. Hardly a difference to be observed.
b. Stability Checks
Being the best of both the worlds, Crank Nicholson provides an improved mechanism of Finite methods, and provides better stablity.
Summary
Market practitioners prefer Crank Nicholson when it somes to Finite Difference techniques. It utilizes the concepts both from Explicit and Implicit Euler methods. Better stability, albeit similar computational requirements as Implicit, Crank Nicholson is a go-to method. A more generalized form is Modified Theta Method (refer to Daniel J Duffy’s book for more details).
Math Concepts
Listing down some of the mathematical concepts referred in this article
- Crank Nicholson Schemes
- Central Difference Technique, Forward Difference techniques
- Tridiagonal Matrices, Sparse Matrix, Matrix algebra
- Modified Theta Method
Appendix
- Research Details & Source: Project Quant, by Ankit Gupta
- Finite Difference Methods in financial engineering, A Partial Differentiation Equation Approach, by Daniel J Duffy
PS: For detailed python notebook, you can reach out to me directly!
Disclaimer: The article is solely made available for educational purposes and doesn't promote any investment or trading guidance whatsoever. Any views or opinions presented in this article are solely those of the author.
