Numerical Methods - Implicit Euler Methods
While the last article, introduced the Euler schemes with Explicit methods, in this article, we will unfold a more advanced method on Implicit Euler Scheme.
Again, starting with the summary of Black Scholes Equation for Call option pricing
Summary of Black Scholes PDE Note In later articles, we will try to value a more complex derivative product, such as Barrier option or a Equity-Credit Hybrid product with a more complex initial value.Backward Black Scholes PDE
$$ % \begin{aligned} -\frac{\partial V}{\partial t'} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 % \end{aligned} $$ Initial Value problem
For a European call option: $$ % \begin{aligned} V(S, 0) = \max(S_T - K, 0) % \end{aligned} $$Boundary Conditions
In the case of boundary conditions, we tend to find option values at extreme ends of stock price. $$ % \begin{aligned} V(0, t) = 0 \\ V(S_{max}, t) = S_{max} - K e^{(-rt)} % \end{aligned} $$
Implicit Euler Scheme - The Theory
Just like the Explicit Euler Scheme, here also, we will follow a trinomial lattice model. However, unlike the Explicit Scheme, where the process at time (t) was dependent on the previous time step (t-1), in Implicit Scheme, the process is dependent on the current time step. It can be better explained in a visual form.

The left panel describes the Explicit Scheme, whereas the right panel highlights Implciit Euler Scheme. Note the difference between these two.
Note
V(i,n+1) depends on 3 points. In order to determine the price at current time and stock price, we need the prices at current time with shocks in the stock price (up and down). That's the crux of Implicit Euler Scheme. And this makes the solution a bit more complex than pure iterations.
- V(i-1, n+1): option value at \( S = S_{i-1} \) and current time
- V(i, n): option value at \( S = S_{i} \) and previous time
- V(i+1, n+1): option value at \( S = S_{i+1} \) and current time
Discretized Black Scholes - Application in Finance
a. Time derivative
Here, \(n+1\) refers to forward in time, using forward difference method —> \(\frac{\partial v}{\partial t'} \approx \frac{v_i^{n+1} - v_i^n}{\Delta t'}\)
b. Spatial derivative (2nd order)
For the second spatial derivative \(\frac{\partial^2 v}{\partial S^2}\), we use the central difference —> \(\frac{\partial^2 v}{\partial S^2} \approx \frac{v_{i+1}^{n+1} - 2v_i^{n+1} + v_{i-1}^{n+1}}{(\Delta S)^2}\)
Important
Note the dependence on n+1, the current time.
c. Spatial derivative (1st order)
For the first spatial derivative \(\frac{\partial v}{\partial S}\), we use the central difference as well —> \(\frac{\partial v}{\partial S} \approx \frac{v_{i+1}^{n+1} - v_{i-1}^{n+1}}{2 \Delta S}\)
d. Black Scholes discretization
Expand for more...
Hence, under the Implicit Euler Scheme, the Backward Black Scholes can be approximated as: $$ % \begin{aligned} -\frac{v_i^{n+1} - v_i^n}{\Delta t} + \frac{1}{2} \sigma^2 S_i^2 \frac{v_{i+1}^{n+1} - 2v_i^{n+1} + v_{i-1}^{n+1}}{(\Delta S)^2} + r S_i \frac{v_{i+1}^{n+1} - v_{i-1}^{n+1}}{2 \Delta S} - r v_i^{n+1} = 0 % \end{aligned} $$ Rearrange this equation to isolate the terms involving \( v^{n+1} \) on left side, and \( v^{n} \) on right side. $$ % \begin{aligned} v_{i-1}^{n+1} (\alpha \Delta t) + v_i^{n+1}(1 - \beta \Delta t) + v_{i+1}^{n+1} (\gamma \Delta t) = v_{i}^{n} % \end{aligned} $$ Wheree. Matrix Formulation
Step 1 - Linear System of Equations
It is easier to visualize the system as a set of equations at \( t = n+1 \), where \( i \) varies from 1 to \( I-1 \). The system can be written as: \[ \begin{aligned} v_{0}^{n+1} (\alpha_1 \Delta t) + v_1^{n+1}(1 - \beta_1 \Delta t) + v_{2}^{n+1} (\gamma_1 \Delta t) &= v_{1}^{n} \\ v_{1}^{n+1} (\alpha_2 \Delta t) + v_2^{n+1}(1 - \beta_2 \Delta t) + v_{3}^{n+1} (\gamma_2 \Delta t) &= v_{2}^{n} \\ v_{2}^{n+1} (\alpha_3 \Delta t) + v_3^{n+1}(1 - \beta_3 \Delta t) + v_{4}^{n+1} (\gamma_3 \Delta t) &= v_{3}^{n} \\ &\vdots \\ v_{I-2}^{n+1} (\alpha_{I-1} \Delta t) + v_{I-1}^{n+1}(1 - \beta_{I-1} \Delta t) + v_{I}^{n+1} (\gamma_{I-1} \Delta t) &= v_{I-1}^{n} \end{aligned} \]Step 2 - Matrix Formulation
This can be conveniently represented in matrix form> as: \( A \cdot X = B \)Where The matrix \( A \) is a tridiagonal matrix of size: (I-1)x(I+1) and is given by: \[ A = \begin{bmatrix} \alpha_1 \Delta t & 1 - \beta_1 \Delta t & \gamma_1 \Delta t & 0 & \cdots & 0 & 0\\ 0 & \alpha_2 \Delta t & 1 - \beta_2 \Delta t & \gamma_2 \Delta t & \cdots & 0 & 0\\ 0 & 0 & \alpha_3 \Delta t & 1 - \beta_3 \Delta t & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & \alpha_{I-1} \Delta t & 1 - \beta_{I-1} \Delta t & \gamma_{I-1} \Delta t \end{bmatrix} \] - The vector \( X \) of unknowns \( v_i^{n+1} \) is displayed as below. It is a vector of size: (I+1): \[ X = \begin{bmatrix} v_0^{n+1} \\ v_1^{n+1} \\ v_2^{n+1} \\ \vdots \\ v_{I-1}^{n+1}\\ v_{I}^{n+1} \end{bmatrix} \] - The vector \( B \) of known values (of size: I-1) from the previous time step is given as below: \[ B = \begin{bmatrix} v_1^n \\ v_2^n \\ v_3^n \\ \vdots \\ v_{I-1}^n \end{bmatrix} \]
Step 3 - Introducing Boundary Conditions
Since boundary conditions are already known to us, we can separate out the \( V_0^{n+1} \) and \( V_I^{n+1} \) terms from left side of the equation. This reduces the matrix set of equations as: \[ \begin{bmatrix} 1 - \beta_1 \Delta t & \gamma_1 \Delta t & 0 & 0 & \cdots & 0 \\ \alpha_2 \Delta t & 1 - \beta_2 \Delta t & \gamma_2 \Delta t & 0 & \cdots & 0 \\ 0 & \alpha_3 \Delta t & 1 - \beta_3 \Delta t & \gamma_3 \Delta t & \cdots & 0 \\ 0 & 0 & \alpha_4 \Delta t & 1 - \beta_4 \Delta t & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & \alpha_{I-1} \Delta t & 1 - \beta_{I-1} \Delta t \end{bmatrix} \begin{bmatrix} v_0^{n+1} \\ v_1^{n+1} \\ v_2^{n+1} \\ \vdots \\ v_{I-1}^{n+1} \end{bmatrix} + \begin{bmatrix} \alpha_1 \Delta t v_0^{n+1} \\ 0 \\ 0 \\ \vdots \\ \gamma_{I-1} \Delta t v_{I}^{n+1} \end{bmatrix} = \begin{bmatrix} v_1^n \\ v_2^n \\ v_3^n \\ \vdots \\ v_{I-1}^n \end{bmatrix} \] Rearranging the above to bring all known terms on right side \[ \begin{bmatrix} 1 - \beta_1 \Delta t & \gamma_1 \Delta t & 0 & 0 & \cdots & 0 \\ \alpha_2 \Delta t & 1 - \beta_2 \Delta t & \gamma_2 \Delta t & 0 & \cdots & 0 \\ 0 & \alpha_3 \Delta t & 1 - \beta_3 \Delta t & \gamma_3 \Delta t & \cdots & 0 \\ 0 & 0 & \alpha_4 \Delta t & 1 - \beta_4 \Delta t & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & \alpha_{I-1} \Delta t & 1 - \beta_{I-1} \Delta t \end{bmatrix} \begin{bmatrix} v_0^{n+1} \\ v_1^{n+1} \\ v_2^{n+1} \\ \vdots \\ v_{I-1}^{n+1} \end{bmatrix} = \begin{bmatrix} v_1^n \\ v_2^n \\ v_3^n \\ \vdots \\ v_{I-1}^n \end{bmatrix} - \begin{bmatrix} \alpha_1 \Delta t v_0^{n+1} \\ 0 \\ 0 \\ \vdots \\ \gamma_{I-1} \Delta t v_{I}^{n+1} \end{bmatrix} \] Once we have the system in this form, it can be solved by solving the linear system \( A \cdot X = B \).Step 4 - Solve the matrix
\( A \cdot X = B \)Important
A is a tridiagonal matrix, and a sparse matrix. More the number of time steps, sparsity increases. We need to ensure that we apply matrix algebra considering the sparsity of A in mind
Codify Implicit Euler - Black Scholes
Here is a sample python code depicting Implicit Euler Scheme:
# relevant libraries for matrix algebra
from scipy import sparse
from scipy.sparse.linalg import spsolve
from importlib import reload
import numpy as np
def ImplicitEuler(SMax, SMin, nbSpaceSteps, timetoMaturity, nbTimeSteps, vol, rate, strike, optiontype = "call"):
# initializing the space and time vectors for the grid
S = np.linspace(SMin, SMax, nbSpaceSteps + 1)
dS = (SMax - SMin)/nbSpaceSteps
time = np.linspace(0, timetoMaturity, nbTimeSteps + 1)
dt = (timetoMaturity - 0)/nbTimeSteps
# setting the storage grid for derivative price
V = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
delta = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
gamma = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
theta = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
# ------ Setting initial condtion
# initial condition
if optiontype.upper()[0] == "C":
V[:,0] = np.maximum(S - strike, 0)
else:
# for put option
V[:,0] = np.maximum(strike - K, 0)
# boundary condition
if optiontype.upper()[0] == "C":
V[0, :] = 0
V[-1, :] = (SMax - strike)*np.exp(-rate*time)
else:
V[-1, :] = 0
V[0, :] = (strike- SMin)*np.exp(-rate*time)
# apply Implicit Euler discretization
I = np.arange(0,nbSpaceSteps+1)
alpha = 0.5 * dt * ((vol**2) * (I**2) - rate*I)
beta = dt * (vol**2 * (I**2) + rate)
gamma = 0.5 * dt * (vol**2 * (I**2) + rate * I)
# Note the usage of sparse matrix using scipy sparse library
ML = sparse.diags([-alpha[2:], 1+beta[1:], -gamma[1:]], [-1,0,1], shape=(nbSpaceSteps-1, nbSpaceSteps-1)).tocsc()
for t in range(1, nbTimeSteps+1):
# loop through time iteratively
boundary_t = np.zeros(nbSpaceSteps - 1)
boundary_t[0] = -alpha[1] * (V[0, t])
boundary_t[-1] = -gamma[nbSpaceSteps - 1] * (V[nbSpaceSteps, t] )
b = V[1:nbSpaceSteps, t - 1] - boundary_t
# Solve the matrix
V[1:nbSpaceSteps, t] = spsolve(ML, b)
return S, time, V
# -------- Compute the call price using implcit euler scheme
SMax = 200
SMin = 0
timetoMaturity = 1
vol = 0.2
rate = 0.05
nbSpaceSteps = 400
nbTimeSteps = 100
strike = 100
S0 = 100
S, _time, callPrice = ImplicitEuler(SMax, SMin, nbSpaceSteps, timetoMaturity, nbTimeSteps, vol, rate, strike, optiontype = "call")
Results
a. Option Valuation
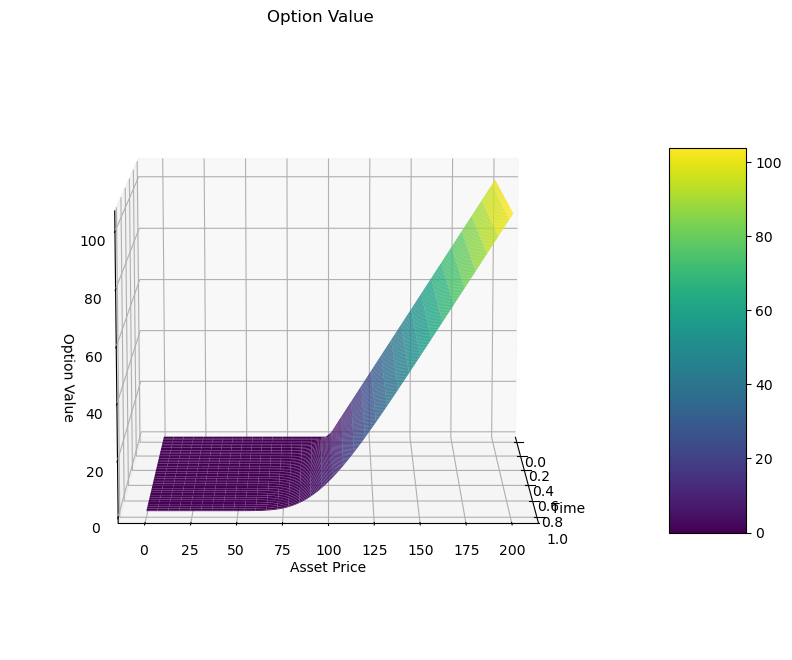
b. Stability Challenges
b.1. Less number of timesteps for computation - Unconditionally stable
 Implicit Methods are unconditionally stable, i.e. irrespective of the time step size, they are stable enough.
Implicit Methods are unconditionally stable, i.e. irrespective of the time step size, they are stable enough.
b.2. Low Volatility - Stable
Again, the stability issues are not so evident 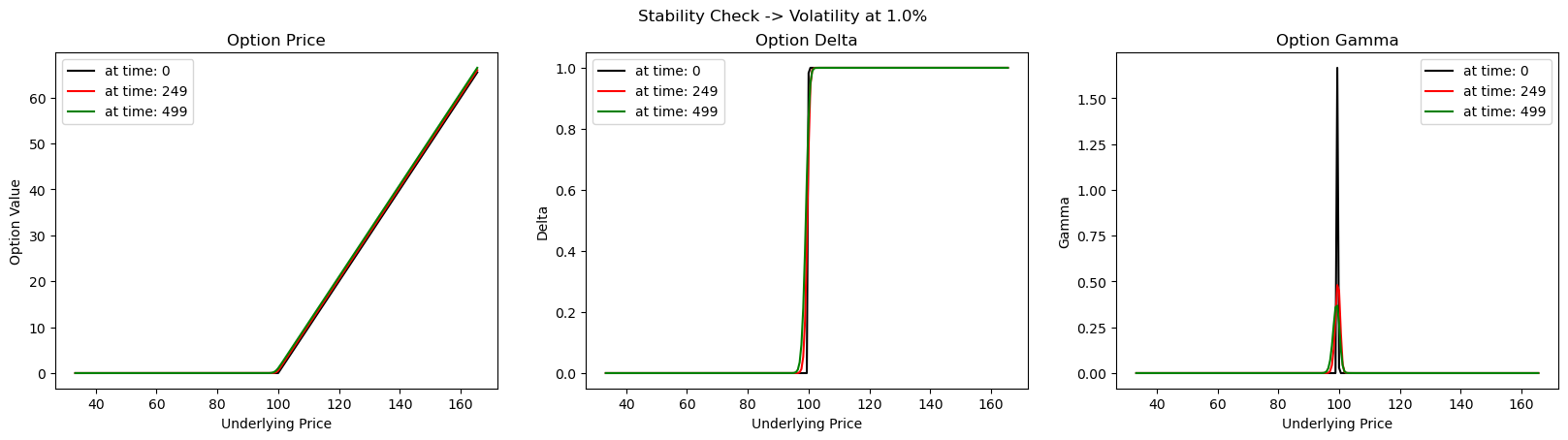
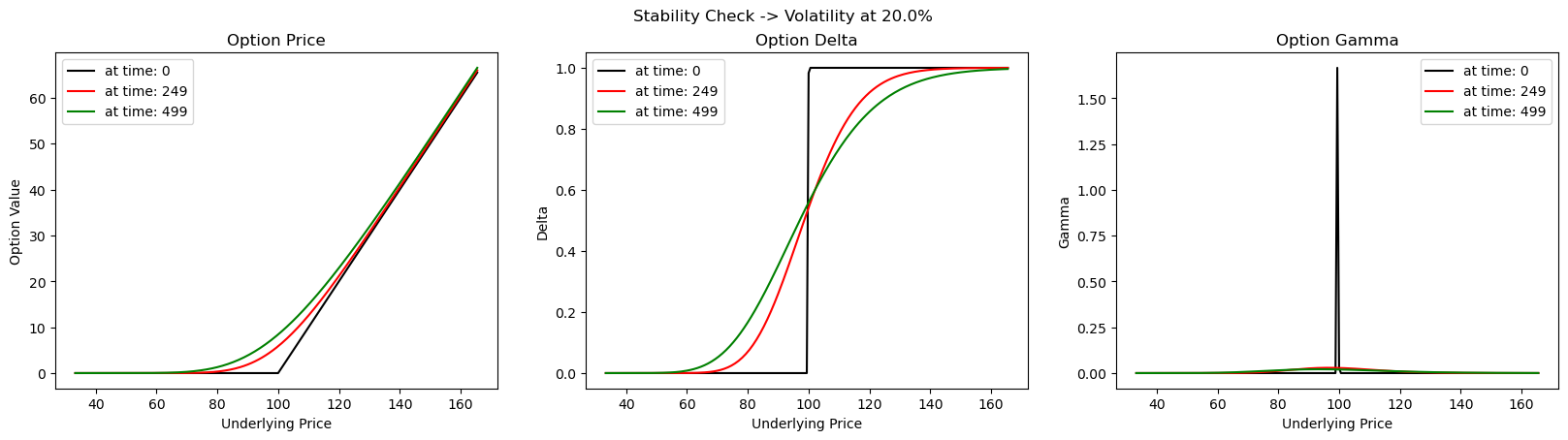
Summary
Implicit Euler Scheme tend to provide more stable solution to the PDE process. Albeit, at a cost of complex implementation. Once the mathematics is understood, the implementation then can be a piece of “cake”.
Math Concepts
Listing down some of the mathematical concepts referred in this article
- Implicit Euler Schemes
- Central Difference Technique, Forward Difference techniques
- Tridiagonal Matrices, Sparse Matrix, Matrix algebra
Appendix
- Research Details & Source: Project Quant, by Ankit Gupta
- Finite Difference Methods in financial engineering, A Partial Differentiation Equation Approach, by Daniel J Duffy
PS: For detailed python notebook, you can reach out to me directly!
Disclaimer: The article is solely made available for educational purposes and doesn't promote any investment or trading guidance whatsoever. Any views or opinions presented in this article are solely those of the author.
