Numerical Methods - Explicit Euler Methods
In the last article, we introduced the concept of Partial Differential equations, and how Black Scholes is a wonderful such example
Starting this article, we will uncover some of the techniques to solve for the Black Scholes equation, i.e. approximating the option values. Note that, for a vanilla call and put option, there is a closed form equation already available which is used in real-world. But the idea of this article to identify techniques which can solve a complex Partial Differential equation.
This article is the 1st of Numerical Methods for solving Partial Differential Equation, with the focus here on Explicit Euler Scheme.
Let’s start with the summary of the Black Scholes PDE.
Summary of Black Scholes PDE Note In later articles, we will try to value a more complex derivative product, such as Barrier option or a Equity-Credit Hybrid product with a more complex initial value.Backward Black Scholes PDE
$$ % \begin{aligned} -\frac{\partial V}{\partial t'} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 % \end{aligned} $$ Initial Value problem
For a European call option: $$ % \begin{aligned} V(S, 0) = \max(S_T - K, 0) % \end{aligned} $$Boundary Conditions
In the case of boundary conditions, we tend to find option values at extreme ends of stock price. $$ % \begin{aligned} V(0, t) = 0 \\ V(S_{max}, t) = S_{max} - K e^{(-rt)} % \end{aligned} $$
Explicit Euler Method - The Theory
Under the Numerical methods, the process is discretized with steps in both space and time. In a simple case of single option pricing, we can have a 2D discretized grid as below, where the y-axis represents possibilities of the stock price movement
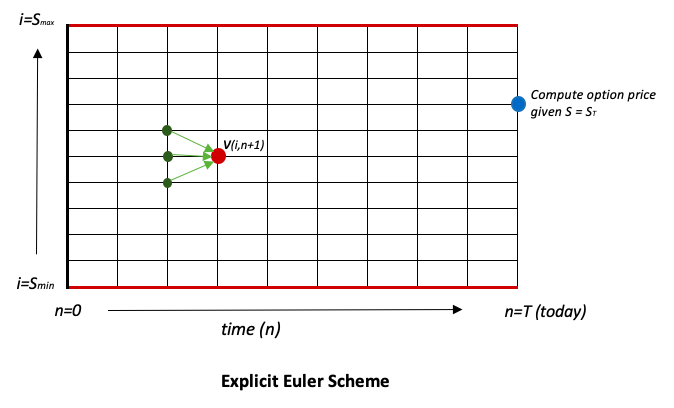
A Vanilla call option pricing can be iteratively done through this grid, given that
- we have the Initial values available at t = 0, i.e. at maturity, and
- boundary conditions are known, i.e, option value when underlying stock is at the extreme.
Note
V(i,n+1) depends on 3 points.
- V(i-1, n): option value at \( S = S_{i-1} \) and previous time
- V(i, n): option value at \( S = S_{i} \) and previous time
- V(i+1, n): option value at \( S = S_{i+1} \) and previous time
Discretized Black Scholes - Application in Finance
a. Time derivative
Here, \(n+1\) refers to forward in time, using forward difference method —> \(\frac{\partial v}{\partial t'} \approx \frac{v_i^{n+1} - v_i^n}{\Delta t'}\)
b. Spatial derivative (2nd order)
For the second spatial derivative \(\frac{\partial^2 v}{\partial S^2}\), we use the central difference —> \(\frac{\partial^2 v}{\partial S^2} \approx \frac{v_{i+1}^{n} - 2v_i^{n} + v_{i-1}^{n}}{(\Delta S)^2}\)
c. Spatial derivative (1st order)
For the first spatial derivative \(\frac{\partial v}{\partial S}\), we use the central difference as well —> \(\frac{\partial v}{\partial S} \approx \frac{v_{i+1}^{n} - v_{i-1}^{n}}{2 \Delta S}\)
d. Black Scholes discretization
Hence, under the Explicit Euler Scheme, the Backward Black Scholes can be approximated as: \[% \begin{aligned} -(\frac{v_i^{n+1} - v_i^n}{\Delta t}) + \frac{1}{2} \sigma^2 S_i^2 \frac{v_{i+1}^{n} - 2v_i^{n} + v_{i-1}^{n}}{(\Delta S)^2} + r S_i \frac{v_{i+1}^{n} - v_{i-1}^{n}}{2 \Delta S} - r v_i^{n} = 0 % \end{aligned}\]
This can be re-written as: \(-{\theta}_i + \frac{1}{2} \sigma^2 S_i^2 {\gamma}_i + r S_i {\delta}_i - r v_i^{n} = 0\)
where
- \({\theta}_i = \frac{v_i^{n+1} - v_i^n}{\Delta t}\) represents how the price changes per unit of time
- \({\delta}_i = \frac{v_{i+1}^{n} - v_{i-1}^{n}}{2 \Delta S}\) represents how price changes per unit of underlying price
- \({\gamma}_i = \frac{v_{i+1}^{n} - 2v_i^{n} + v_{i-1}^{n}}{(\Delta S)^2}\) represesnts how delta changes per unit of price
Hence, \(v_i^{n+1} = v_i^n + \Delta t.\theta\)
Codify Explicit Euler - Black Scholes
Above discretization steps help compute the value of \(v_i^{n+1}\) at time step \(n+1\). The entire process needs to execute iteratively across values of time ranging till t = \(T\). Within each time step, we need to iterate through each space step as well. Here is a sample python code depicting Explicit Euler Scheme:
SMax = 200
SMin = 0
timetoMaturity = 1
vol = 0.2
rate = 0.05
nbSpaceSteps = 100
nbTimeSteps = 100
K = 100 # strike
S0 = 100
# initializing the space and time vectors for the grid
S = np.linspace(SMin, SMax, nbSpaceSteps + 1)
dS = (SMax - SMin)/nbSpaceSteps
t = np.linspace(0, timetoMaturity, nbTimeSteps + 1)
dt = (timetoMaturity - 0)/nbTimeSteps
# setting the storage grid for derivative price
V = np.zeros((nbSpaceSteps+1, nbTimeSteps+1))
# initial condition
if optiontype.upper()[0] == "C":
V[:,0] = np.maximum(S - strike, 0)
else:
# for put option
V[:,0] = np.maximum(strike - K, 0)
# boundary condition
if optiontype.upper()[0] == "C":
V[0, :] = 0
V[-1, :] = (SMax - strike)*np.exp(-rate*t)
else:
V[-1, :] = 0
V[0, :] = (strike- SMin)*np.exp(-rate*t)
# apply Explicit Euler discretization
for n in range(0, nbTimeSteps):
# time refers to time to maturity
for i in range(1, nbSpaceSteps):
# compute intermediaries
_delta = (V[i+1, n] - V[i-1, n])/(2*dS)
_gamma = (V[i+1, n] - 2*V[i, n] + V[i-1, n])/(dS*dS)
_theta = -0.5*vol**2*S[i]**2*_gamma - rate*S[i]*_delta + rate*V[i,n]
V[i, n+1] = V[i, n] - dt*_theta
Results
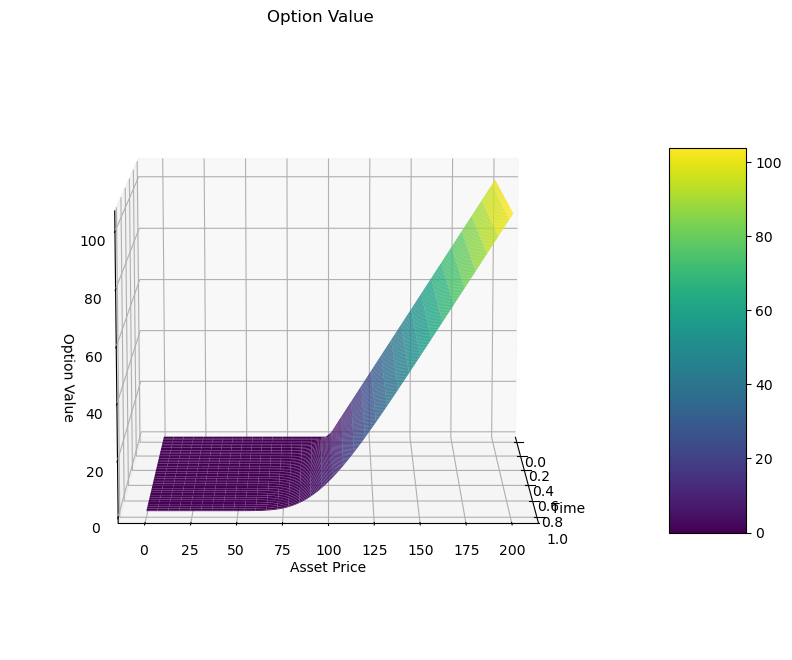
a. Option Valuation
A vanilla call option is, as the name suggests, “Vanilla”. Similar valuation can be obtained through the closed form equation for Call option. However, in the later articles we will extend the techniques to price more complex derivatives.
b. Stability Challenges
Well, Explicit Euler Scheme behaves erratically for certain cases. b.1. Less number of timesteps for computation
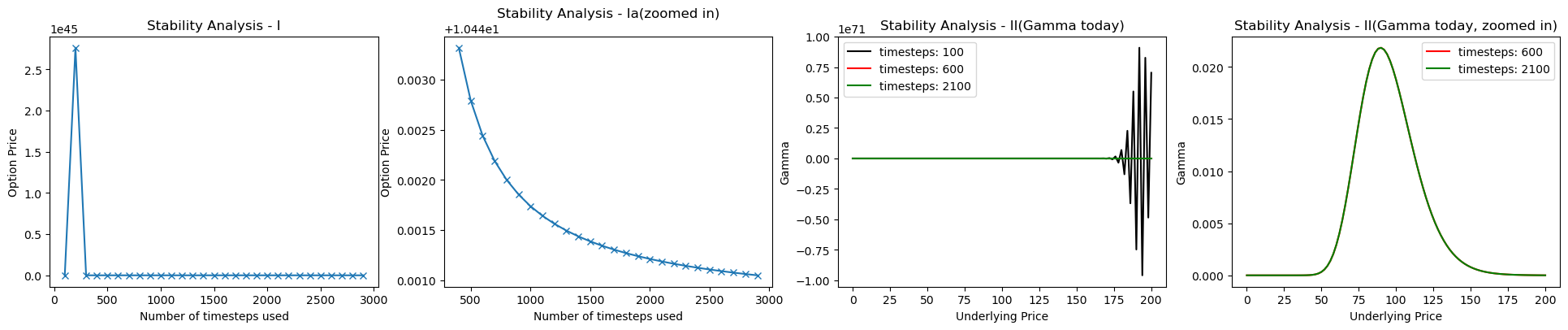As step size, _dt_, increases (or timesteps decrease), stability concerns start arising. Computation of the option price becomes extremely unstable. Figure (i) displays how the option price significantly fluctuates before getting more stable once timesteps increase. Similarly, Figure (iv) tells the story about gamma. Gamma (second order derivative) compuation fluctuates at the boundary values of underlying price. b.2. Low Volatility
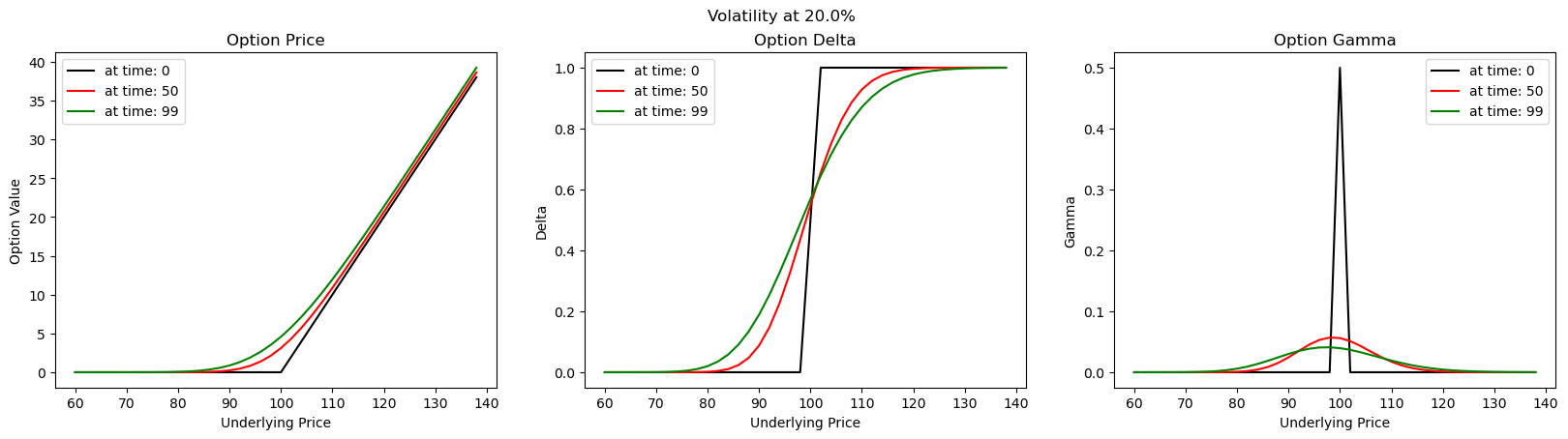
As volatiliy decreases (or diffusion component decreases), Explicit Euler scheme tends to render itself as useless. In the case of FX derivatives, where volatility tends to be usually in single digits, this scheme may not be the best. At a volatility level of 0.1% (extremely low vol), the unstability is clearly evident near the strike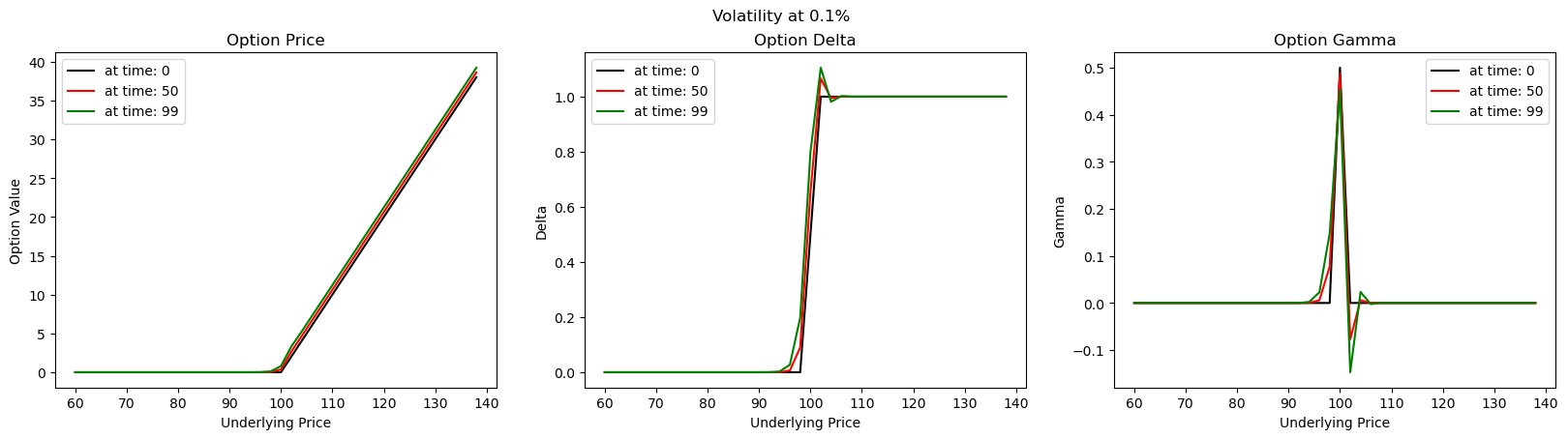
As volatility goes up, we tend to obtain a more stabile profile of price and risk profiles.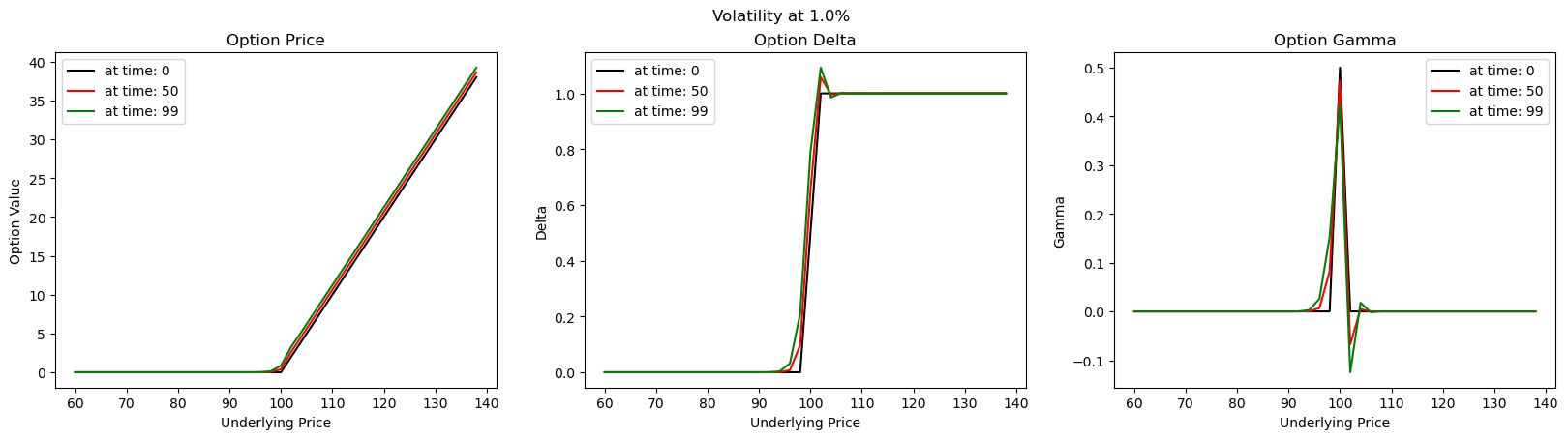
Summary
Explicit Euler Scheme is the most basic of Numerical Methods of solving Partial Differential Equations. Although simplistic, both in understanding and python implementation, this scheme comes with quite a few limitations, and hence a lower practical usage. In the next article, I will focus on another version of Euler methods.
Math Concepts
Listing down some of the mathematical concepts referred in this article
- Explicit Euler Schemes
- Central Difference Technique, Forward Difference techniques
- Trinomial Pricing (lattice models)
Appendix
- Research Details & Source: Project Quant, by Ankit Gupta
- Finite Difference Methods in financial engineering, A Partial Differentiation Equation Approach, by Daniel J Duffy
PS: For detailed python notebook, you can reach out to me directly!
Disclaimer: The article is solely made available for educational purposes and doesn't promote any investment or trading guidance whatsoever. Any views or opinions presented in this article are solely those of the author.